Boundary Preserving Dense Local Regions

Jaechul Kim and Kristen Grauman

[pdf] [code] [slides]

Motivation

Good features to match images: Repeatable across the images and distinctive among the features.

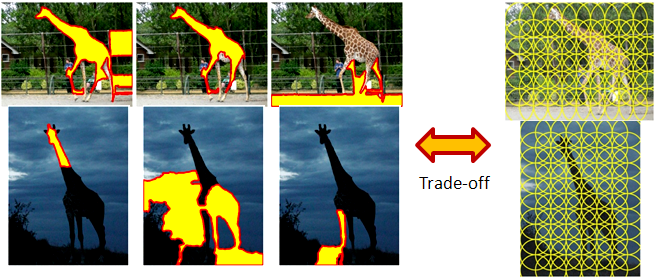
  Trade-off of distinctiveness and repeatability of existing features.                                 
                  Distinctive but not repeatable (Segmented regions)                   Repeatable but not distinctive (Dense patch sampling)
                                            Figure 1. Trade-off of distinctiveness and repeatability of existing features.

Boundary Preserving Local Regions (BPLRs)

Example detections of BPLRs.   
                                                      Figure 2. Example detections of BPLRs.

- BPLRs respect object boundaries, capturing object's local shape.
- BPLRs are densely extracted in a regular grid across the image, although Figure 2 shows only a fraction of extracted regions for display.
- Dense and shapre-preserving properties make BPLRs both repeatble and distinctive.
- To obtain BPLRs, we propose a novel feature sampling and linking strategy driven by multiple segmentation.

BPLR's Key Contrast

    Illustration of BPLR's key constrasts with representative existing detectors.
             (a) BPLR                                      (b) Segmented regions                                               (c) Superpixels                             (d) MSER            (e) Dense sampling
Figure 3. Illustration of BPLR's key constrasts with representative existing detectors. Existing detectors lack either repeatability or distinctiveness, or even both. On the other hand,
the proposed BPLRs captures object’s local shape in a repeatable manner under image variation like appearance and background clutter. (Note, for BPLRs we display only a sample
for different foreground object parts; our complete extraction is dense and covers entire image.)

Approach

- Overview

Our method consists of three major components: 1) sampling base features, which we call "elements", from each segment of a pool of multiple segmentations,
2) linking the sampled elements into a single graph across the image, and 3) grouping neighbor elements in the graph to form BPLRs.

                      Initial elements for one segment              Minimum spanning tree                 Edge removed               Grouped elements  -->   One BPLR  -->    Descriptor   
           Sampling elements   Linking elements across the image  Grouping neighbor elements into BPLRs    
                               (a) Sampling elements                                         (b) Linking elements across the image                                  (c) Grouping neighbor elements into BPLRs
Figure 4. Main components of the approach. (a) For each initial segment from a pool of multiple segmentations, we sample local elements densely in a grid according to its distance transform
(left: segment; lower right: grid; upper right: zoom-in to show sampled elements and their scales). (b) Elements are linked across the image, using the overlapping multiple segmentations to create
a single structure that reflects the main shapes and segment layout. (c) Using that structure, we extract one BPLR per element. Each BPLR is a group of neighboring elements. Finally, the BPLR
is mapped to some descriptor (we use PHOG+gPb).

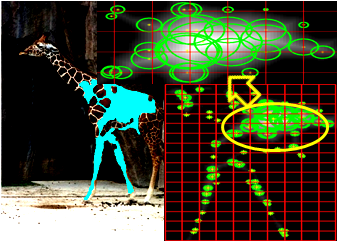
- Sampling

The first step of our method is to sample elements from each segment of the input segmentations.
Given a segment, we compute distance transform from the boundary of the segment and divide the segment into regular grid cells.
At each grid cell, we sample an element at the location with the maximal distance transform value within the cell (Figure 5 (b)).
The sampled element is represented by a circle; its center is the sampled location and its radius, the element's scale, is given by that maximal distance transform value at the sample position (Figure 5(c)).

Our distance transform (DT)-based sampling has two geometric properties:
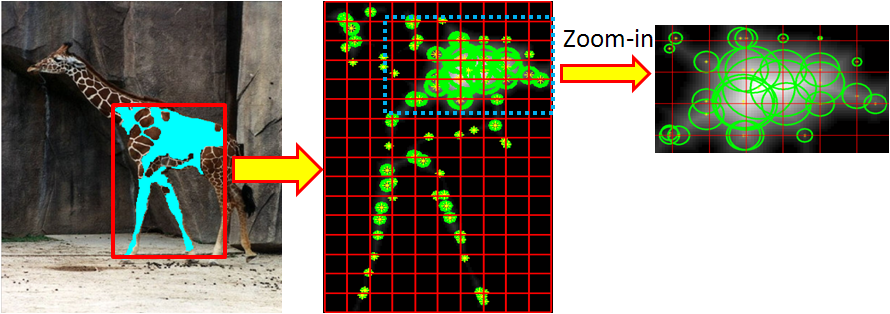
Sampling elements in a segment.
            (a) One segment                              (b) Sampling at dense grids                 (c) Zoom-in view of sampled elements
                                                             Figure 5. Sampling elements in a segment.

- Linking

Given sampled elements from all segments, we link them into a single graph structure. We compute a global linkage graph connecting all element locations via a minimum spanning tree,
where each edge weight is given by the Euclidean distance between the two points it connects. By minimizing the sum of total edge weights, the resulting spanning tree removes
the longer edges from the graph—most of which cross object boundaries due to the "concentrating effect" of the DT-based sampling (Figure 6(a)).
Note, although our linking method favors linkages among same-segment elements, linkages are not restricted to each single segment by overlapping multiple segments.

Whereas the minimum spanning tree reduces connectivity for more distant elements, we also want to reduce connectivity for elements divided by any apparent object contours.
Thus, in the second linkage step, we compute a simple post-processing of the spanning tree that removes noisy tree edges that cross strong intervening contours (we use gPb for contour detection).
Figure 6(b) shows the types of links removed by this post-processsing; we see that most do indeed cross object boundaries.

Minimum spanning tree              Spurious tree edges removed by post-processing
       (a) Minimum spanning tree                  (b) Spurious tree edges removed by post-processing
                                       Figure 6. Linking elements across the image

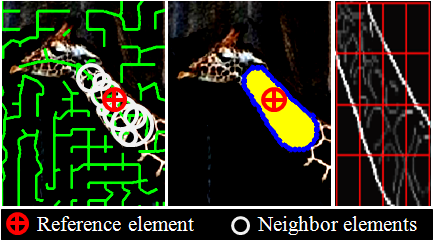
- Grouping

Finally, we group neighbor elements for each element in the graph, which forms BPLR of the element.Given an element, we define its topological neighbors within N hops from the element.

And, we also define its Euclidean neighbors within F times the scale of the element. Intersection of topological and Euclidean neighbors forms a BPLR of the element, and we represent a BPLR with a descriptor.

Any existing descriptors can be used; in our experiment we used PHOG with gPb edge for descriptor.We repeat the same procedure for all elements in the graph, obtaining dense extraction of BPLRs.

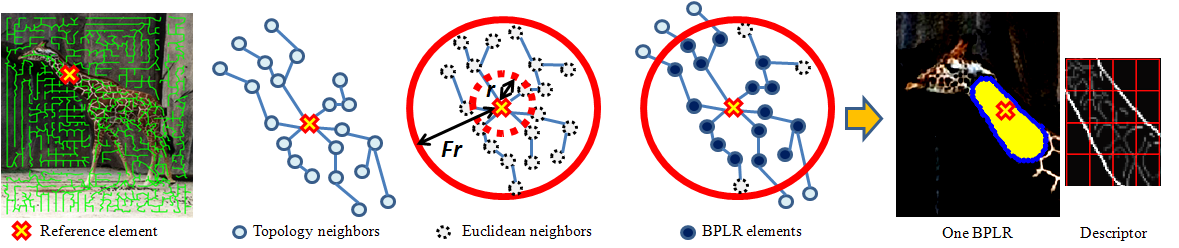
Grouping neighbor elements into a BPLR for a reference element.

Figure 7. Grouping neighbor elements into a BPLR for a reference element. Topology neighbors: up to N(= 3) hops for the reference; Euclidean neighbors: within F times the scale of the reference;
BPLR elements: intersection of topology and Euclidean neighbors. Every extracted BPLR is represented by a descriptor, for which we use PHOG + gPb in the experiment.

Results

We made experiments to evaluate raw feature quality of BPLR compared to existing feature detectors.
Then we apply it to foreground discovery and object classification to show its effectiveness when used for tasks that require reliable feature matching.

- Repeatability

First, we test repeatability of feature for object category matching. To measure repeatability, we use Bounding Box Hit Rate - False Positive Rate (BBHR-FPR) metric introduced by Quack et.al.
It evaluates how well foreground features on an object match other foreground features in the same class.
We compare BPLR to existing region detectors, including dense sampling, local interest operator (MSER), and segmented regions.
In addition, we compare BPLR to semi-local features which use class-specific supervision to find geometric configurations of local features common to the class.
Figure 8 and 9 show BPLR outperforms all the baselines.
 
            Repeatability on ETHZ shape objects.           
Figure 8. Repeatability on ETHZ shape objects. Plots compare BPLR to three alternative region detectors: MSER, dense sampling, and segments. Quality is measured by the bounding box hit rate-false positive rate (BBHR-FPR).
Curves that are lower on the y-axis (fewer false positives) and longer along the x-axis (higher hit rate) are better.
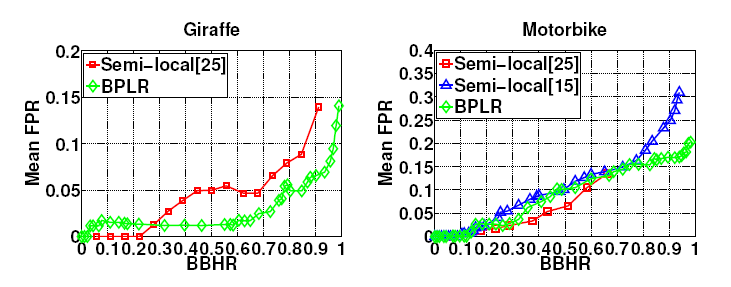
                                                                          Repeatability on ETH+TUD objects.                                                                         
Figure 9. Repeatability on ETH+TUD objects. Plots compare BPLR to two state-of-the-art semi-local feature methods [25, 15]. ([15]  does not report results on the Giraffe class.)

- Localization Accuracy

Second, we evaluate localization accuracy of feature matching. To measure localization accuracy, we introduce Bounding Box Overlap Score - Recall (BBOS-Recall) metric. 
It evaluates how accurately feature matches can predict objects’ positions and scale as shown in Figure 10.

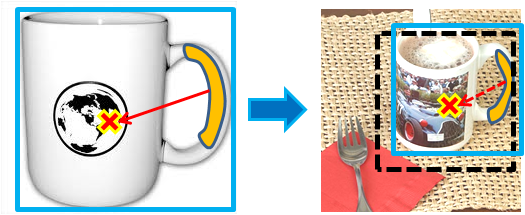
                                                              How to compute BBOS                                                             
                                                                           Training image                                    Test image
Figure 10. Given two matched regions and their relative scales, we project the training exemplar’s bounding box into the test image (dotted rectangle).
That match’s BBOS is the overlap ratio between the projected box and the object’s true bounding box.

In Figure 11, we see BPLR provides better localization accuracy, verifying the distinctiveness of BPLR by capturing object’s local shape.
In addition, Figure 12 shows example matches of BPLR, illustrating BPLR's localization power. In this example, we automatically select the top five non-overlapping regions based on the nearest-neigbor matching distance.
Leftmost image at each row is the test image and remaining images are training images which have the best matches for the test BPLRs. Same colors indicate matched regions.

            Localization accuracy on ETHZ shape objects.             
Figure 11. Localization accuracy on ETHZ shape objects. Plots compare our approach (BPLR) to three alternative region detectors: MSER, dense sampling, and segments. Quality is measured by the bounding box overlap score - recall (BBOS-Recall),
which captures the layout of the feature matches. Curves that are higher in the y-axis (better object overlap) and longer along the x-axis (higher recall) are better.


Example matches showing BPLR’s localization accuracy.
Figure 12. Example matches showing BPLR’s localization accuracy. Colors in the same row indicate matched regions.

- Foreground Discovery

We apply BPLR to weakly-supervised foreground discovery, in which the system is given a set of cluttered images that all contain the same object class,
and must estimate which pixels are foreground.
In this experiment, we aim to show that BPLR is effective for segmentation in place of superpixels, which is widely used for segmentation.
For foreground discovery, we implement GrabCut where we replace superpixels by BPLRs and use BPLR matching scores to estimate the foreground.
Our BPLR-based GrabCut implementation achieves the state-of-the-art performance.

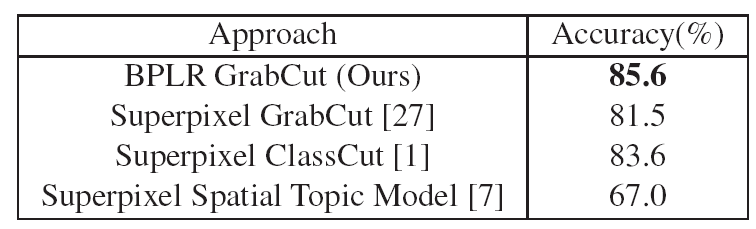
                                                    Foreground discovery results                                               
Table 1. Foreground discovery results, compared to several state-of-the-art methods. Using BPLR regions with a GrabCut-based solution, we obtain
the best accuracy to date on the Caltech-28 dataset.

Example foreground discovery results using BPLRs.
                         Figure 13. Example foreground discovery results using BPLRs. Two examples per class. Ground truth is marked in red.

- Object Classification

Lastly, we apply our features to object recognition on the Caltech-101. We employ a relatively simple classification model on top of the BPLRs, to help isolate their
impact. Specifically, we use the Naive Bayes Nearest-neighbor (NBNN) classifier by Boiman et.al.
Table 2 compares BPLR to alternative feature extractors using NBNN with identical parameter settings. BPLRs outperforms the baselines.


Table 3 compares to existing nearest neighbor-based results: we are among the leading accuracy. BPLRs outperforms the baselines.BPLRs outperforms the baselines.
 
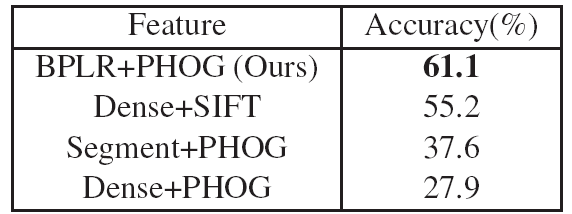
                                         Direct comparison of BPLR to other feature detectors on the Caltech-101                                    
Table 2. Direct comparison of BPLR to other feature detectors on the Caltech-101 (15-15 training/test images).
The only thing varying per method is the feature extractor, and our method provides the most accurate results.

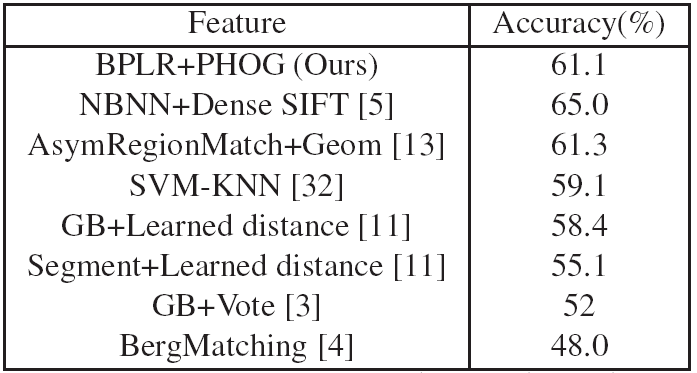
                              Comparing to existing Caltech-101 numbers
Table 3. Comparison to existing results on the Caltech-101 that use nearest neighbor-based classifiers.

Conclusions

We proposed a novel segmentation-driven feature sampling and linking strategy to produce repeatable shape-preserving local regions. As shown through extensive experiments, the key characteristics that distinguish BPLR from existing detectors are:
  • it can improve the ultimate descriptors’ distinctiveness, while still retaining thorough coverage of the image,
  • it exploits segments’ shape cues without relying on them directly to generate regions, thereby retaining robustness to segmentation variability, and
  • its generic bottom-up extraction makes it applicable whether or not prior class knowledge is available.

Publication

Jaechul Kim and Kristen Grauman, Boundary Preserving Dense Local Regions, In Proc. International Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2011. [pdf] [slides]

Code

To download the code, you can check out this page: [code download]