Hashing Hyperplane Queries to Near Points with Applications to Large-Scale Active Learning
Prateek Jain , Sudheendra Vijayanarasimhan
, Sudheendra Vijayanarasimhan , and Kristen Grauman
, and Kristen Grauman
Microsoft Research Lab, Bangalore, INDIA ,
,
University of Texas, Austin, TX, USA
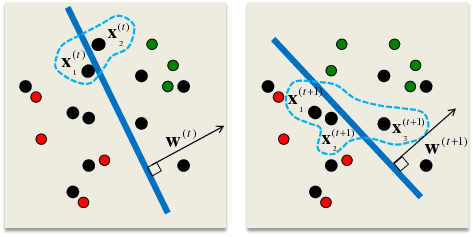
Goal: For large-scale active learning, want to repeatedly query annotators to label the most uncertain examples in a massive pool of unlabeled data
 .
.
Margin-based selection criterion for SVMs [Tong & Koller, 2000] selects points nearest to current decision boundary:
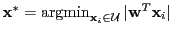
Problem: With massive unlabeled pool, we cannot afford exhaustive linear scan.
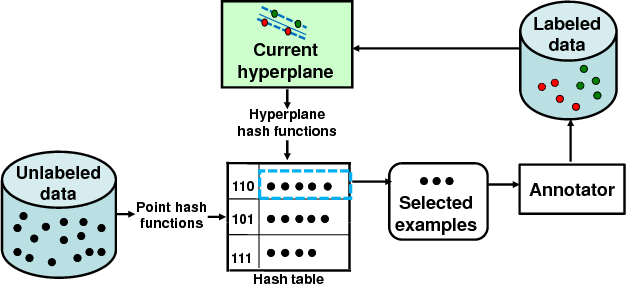
Idea: We define two hash function families that are locality-sensitive for the nearest neighbor to a hyperplane query search problem. The two variants offer trade-offs in error bounds versus computational cost.
- Offline: Hash unlabeled data into table.
- Online: Hash current classifier as ``query" to directly retrieve next examples for labeling.
Main contributions:
- Novel hash functions to map query hyperplane to near points in sub-linear time.
- Bounds for locality-sensitivity of hash families for perpendicular vectors.
- Large-scale pool-based active learning results for documents and images, with up to one million unlabeled points.
Let
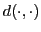 be a distance function over items from a set
be a distance function over items from a set 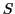 , and for any item
, and for any item 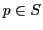 , let
, let 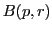 denote the set of examples from
denote the set of examples from 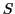 within radius
within radius 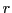 from
from 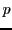 .
.
Definition:
Let
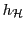 denote a random choice of a hash function from the family
denote a random choice of a hash function from the family 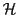 . The family
. The family 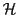 is called
is called
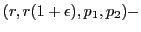 sensitive for
sensitive for
 when, for any
when, for any
 ,
,
Algorithm:
- Compute
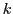 -bit hash keys for each point
-bit hash keys for each point 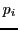 :
:
![$ \left[h_{\cal{H}}^{(1)}(p_i),h_{\cal{H}}^{(2)}(p_i),\dots,h_{\cal{H}}^{(k)}(p_i)\right]$](img21.png) .
.
- Given a query
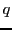 , search over examples in the
, search over examples in the 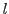 buckets to which
buckets to which 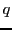 hashes.
hashes.
- Use
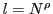 hash tables for
hash tables for 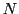 points, where
points, where
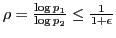 ,
,
- A
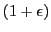 -approximate solution is retrieved in time
-approximate solution is retrieved in time
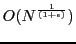 .
.
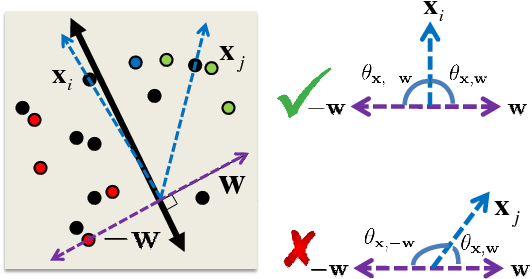
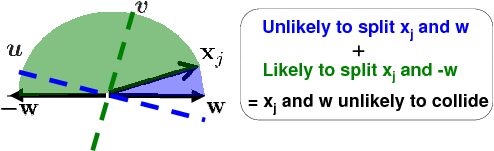
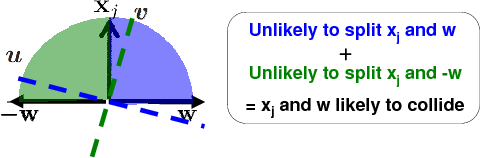
Intuition: To retrieve those points for which
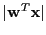 is small, we want collisions to be probable for vectors perpendicular to hyperplane normal (assuming normalized data).
For
is small, we want collisions to be probable for vectors perpendicular to hyperplane normal (assuming normalized data).
For
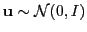 ,
,
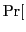 sign
sign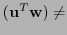 sign
sign![$ (\u ^T\mathbf{x})]=\frac{1}{\pi} \theta_{\mathbf{w},\mathbf{x}}$](img33.png) [Goemans & Williamson, 1995].
[Goemans & Williamson, 1995].
Our idea: Generate two independent random vectors 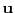 and
and 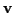 : one to capture angle between
: one to capture angle between
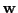 and
and
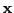 , and one to capture angle between
, and one to capture angle between
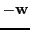 and
and
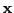 .
.
Definition: We define H-Hash function family
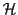 as:
as:
where
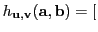 sign
sign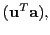 sign
sign![$ (\v ^T\b )],$](img43.png) is a two-bit hash, and
is a two-bit hash, and
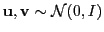 .
.
Analysis:
Intuition: Design Euclidean embedding after which minimizing distance is equivalent to minimizing
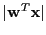 , making existing approx. NN methods applicable.
, making existing approx. NN methods applicable.
Definition: We define EH-Hash function family
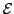 as:
as:
where
![$ V(\mathbf{a}) = {\text vec}(\mathbf{a}\mathbf{a}^T)=\left[a_1^2, a_1a_2, \dots, a_1a_d, a_2^2, a_2a_3, \dots, a_d^2\right]$](img50.png) gives the embedding, and
gives the embedding, and
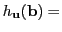 sign
sign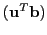 , with
, with
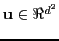 sampled from
sampled from
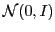 .
.
Analysis:
- Since
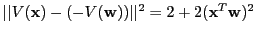 , distance between embeddings of
, distance between embeddings of
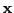 and
and
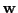 proportional to desired distance, so standard LSH function
proportional to desired distance, so standard LSH function
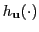 applicable.
applicable.
- We have
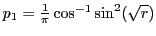 . Hence, sub-linear time search with about twice the
. Hence, sub-linear time search with about twice the 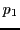 guaranteed by H-Hash.
guaranteed by H-Hash.
Issue:
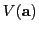 is
is 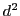 -dimensional, higher hashing overhead.
-dimensional, higher hashing overhead.
Solution: Compute
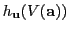 approximately using randomized sampling:
approximately using randomized sampling:
H-Hash has faster pre-processing, but EH-Hash has stronger bounds.
| |
Accuracy |
Hashing insertion time |
| H-Hash: |
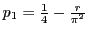 |
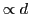 |
|---|
| EH-Hash: |
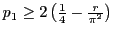 |
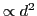 ( (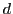 with sampling) with sampling) |
|---|
Goal: Show that proposed algorithms can select examples nearly as well as the exhaustive approach, but with substantially greater efficiency.
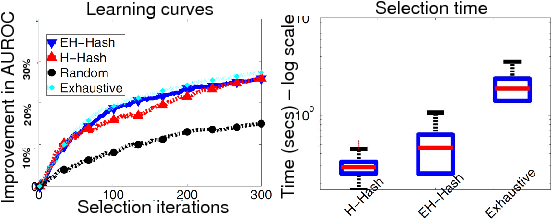
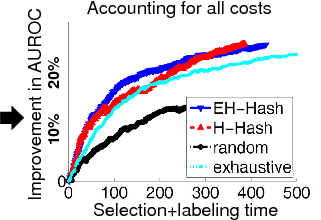
Newsgroups: 20K documents, bag-of-words features.
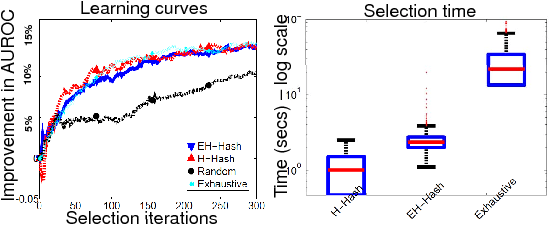
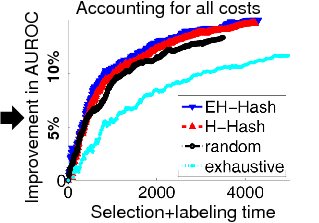
Tiny Images: 60K-1M images, Gist features.
- Accounting for both selection and labeling time, our approach performs better than either random selection or exhaustive active selection.
- Trade-offs confirmed in practice: H-Hash faster, EH-Hash more accurate.
- In future work, we plan to explore extensions for non-linear kernels.
Hashing Hyperplane Queries to Near Points with Applications to Large-Scale Active Learning,
P. Jain, S. Vijayanarasimhan and K. Grauman, in NIPS 2010
[paper, supplementary]
![]() , Sudheendra Vijayanarasimhan
, Sudheendra Vijayanarasimhan![]() , and Kristen Grauman
, and Kristen Grauman![]()
![]() ,
,
![]()
![]() denote a random choice of a hash function from the family
denote a random choice of a hash function from the family ![]() . The family
. The family ![]() is called
is called
![]() sensitive for
sensitive for
![]() when, for any
when, for any
![]() ,
,
![]() and
and ![]() : one to capture angle between
: one to capture angle between
![]() and
and
![]() , and one to capture angle between
, and one to capture angle between
![]() and
and
![]() .
.
![]() as:
as:
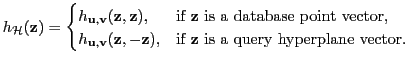
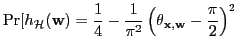
![]() , making existing approx. NN methods applicable.
, making existing approx. NN methods applicable.
![]() as:
as:
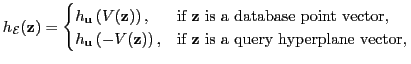
![]() is
is ![]() -dimensional, higher hashing overhead.
-dimensional, higher hashing overhead.
![]() approximately using randomized sampling:
approximately using randomized sampling:



